






At TradeWraps, our Vehicle Wrap AND Upfitting company in Manassas, VA, specializes in getting your business graphics on cars and trucks that create engaging mobile advertising for your business. We also offer Upfitting, so you can get your graphics, and your locks, shelves, and storage solutions, all at the same place! With our proven process, we can deliver the kind of quick and effective results that your fleet needs. We’re your one stop shop for Vehicle Wraps and Upfitting!













Our Solutions
Empower Your Brand with TradeWraps, the Wrap & Upfitting Professionals!
Smart business owners use the spaces available to them to interact with existing and potential customers in meaningful ways. Two often-overlooked, high-impact areas for messages are your windows and floors. Custom floor graphics and window graphics create effective, affordable opportunities to engage with your audience.
Your walls are large, blank canvasses with countless possibilities to showcase your business and attract more customers. With a carefully planned and executed wall mural, you can take full advantage of this unique chunk of real estate. Let TradeWraps help with this project!
Architectural wraps offer an affordable way to brand, customize or simply redecorate your space. Plus, they’re easy to change when you’re ready for a facelift. They help make your environment clean, comfortable and inviting while portraying your company personality.
Why Vehicle Wraps?
Fleet graphics don't cost you per impression, like ads typically do. It's almost like free advertising.
Studies show that on average, Americans spend 20 hours a week on the road. Often they'll come across wrapped trucks, vans, and cars on the way to wherever their destination is.
When parked at a job-site, potential clients won't need to shop around, they see the bold wrapped vehicle and immediately know who to call!

At One Shop
One-Stop Shop
TradeWraps does Upfitting!
At TradeWraps, we know how tough it can be to schedule your new vehicle with both your upfitter, and your wrapper, that’s why we’ve partnered with Ranger Design and Legend to give you the same quality service, at one place!
We're beyond impressed with Ranger Design's extensive commercial vehicle storage and shelving solutions for all different trades, plumbing, HVAC, electrical, you name it! They even had a 3D tool we use to fully customize your upfitting!
Legend not only offers comfortable and quiet flooring, a convenient side step, and insulated wall liners, but they also are the creator of the Securilock Slamlock, the only unbreakable and unbreachable van lock on the market right now!
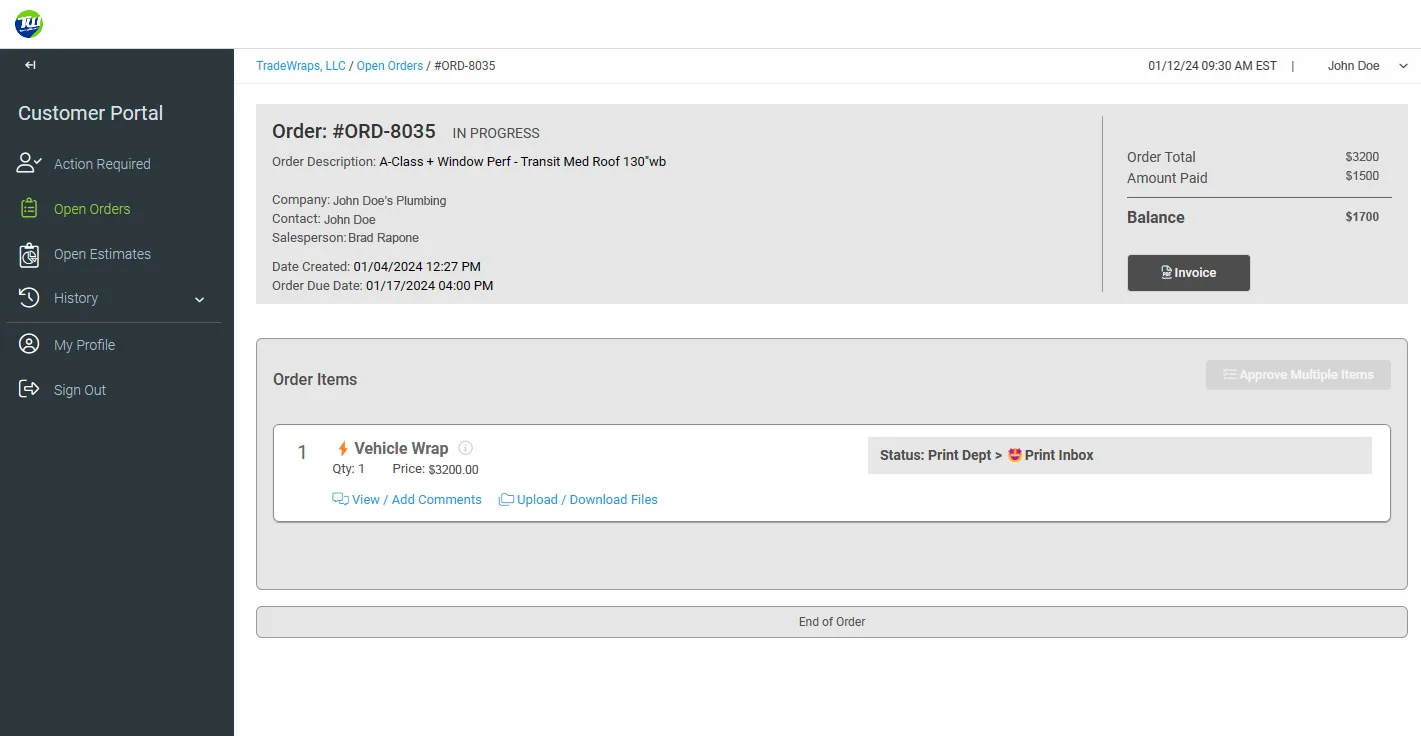
Always have access to your order progress and remaining balances!
No need to call
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
How it works
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Strategy Consultation and Goal Setting
Augue ante tortor mi purus aenean etiam. Nam suspendisse nunc taciti augue euismod risus. Porttitor aenean felis tristique volutpat natoque in phasellus tortor quam vestibulum eleifend.
Data-Driven Analysis and Content Planning
Augue ante tortor mi purus aenean etiam. Nam suspendisse nunc taciti augue euismod risus. Porttitor aenean felis tristique volutpat natoque in phasellus tortor quam vestibulum eleifend.


Execution and Optimization
Augue ante tortor mi purus aenean etiam. Nam suspendisse nunc taciti augue euismod risus. Porttitor aenean felis tristique volutpat natoque in phasellus tortor quam vestibulum eleifend.

Client Feedback & Reviews





Why Choose Us
TradeWraps is second to none when it comes to design, quality, speed and customer service. From the initial consultation to the finished product, we have a proven process and will walk you through it—every step of the way. The end result is a top quality wrap that will dazzle beyond your wildest expectations.
Effective wrapping requires a compelling design that captivates attention and conveys clear messages. Our skilled designers excel in understanding your preferences and expectations, ensuring a successful outcome in both printing and installation.
A TradeWraps, we utilize advanced latex printing and reliable Avery wrap films to ensure top-notch quality. Unlike others who compromise with subpar products and unqualified installers, we remain dedicated to our process, guaranteeing that every wrap is executed with excellence, minimizing the risk of damage to your vehicles.
We’re keenly aware that your vehicles are a major source of revenue. We will work closely with you to make sure your vehicles are wrapped and back on the road as quickly as possible.
Our customer service representatives are determined to make sure you have the best experience possible with TradeWraps. They are friendly, knowledgeable and accessible. They will answer all of your questions, provide a quote and even schedule your installation dates.
Featured Project
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
TradeWraps
Trust the Wrap & Upfitting Professionals!
Click the button below for a quote, OR, Text us using that icon on the lower right corner of the screen!

